Constructivism is “an approach to learning that holds that people actively construct or make their own knowledge and that reality is determined by the experiences of the learner” (Elliott et al., 2000:256). A celebrated idea in education, constructivism has been around for a long time.
Teaching math through constructivist methods allows students to deepen their knowledge beyond rote memorization, develop meaningful context to comprehend the content, and take command of the learning process as an active participant rather than a sit-and-get observer.
Trust the data. Constructivist learning works and pays dividends on students' ability for their entire life.
Pedagogical Origins
There are three schools of constructivist teaching—cognitive constructivism, social constructivism, and radical constructivism. Despite the differences in these schools of thought, five core principles underlie them all:
- Knowledge is constructed: Using our prior knowledge, we build new knowledge by drawing comparisons and making connections. In math this means we use foundational concepts to build the next one (e.g., we learn to add by counting and multiply by adding repeatedly).
- Active learning:A To learn, students must be part of the process (e.g., problem-solving, productive struggle, debate, etc.) in order to understand new content; students can receive new information passively (e.g., being lectured to), but this pales in comparison to understanding it through direct, active participation.
- Social learning: We learn best by doing something together and interacting with it socially; our social behaviors and habits influence how we think about what we learn.
- Knowledge is personal: Subjectivity of experience dictates that we each will differ in how we learn and comprehend a given concept.
- Reality and the mind: Received knowledge is both socially tempered and subjective in nature; as it is exclusively a process of the mind, we must agree that knowledge molds our perception of reality. As we learn more, we update our mental models of the world, thus changing how we see and interpret reality.
What does this mean for the teacher? Traditional classrooms, or direct-instruction classrooms, are often teacher-focused; look no further than a college lecture hall to see an example. The teacher lectures; the students listen. A constructivist teacher behaves radically differently. The table below shows a comparison and example of the two styles:
|
Traditional Classroom |
Example |
Constructivist Classroom |
Example |
|
Knowledge exists outside the student |
Books, lectures, videos act as the repository of knowledge |
Knowledge exists within the student |
Students interpret materials to develop their own meaning and understanding |
|
Teacher-centered |
Primarily teacher lecture and teacher-interest used to create activities |
Student-centered |
Student voice and interest is part of the curriculum |
|
Passive learners |
Sit-and-get |
Active learners |
Students use inquiry and discovery to learn |
|
Individual activities |
Worksheets, readings, and tests |
Interactive activities |
Hands-on investigation, debate, and creativity |
|
Competitive |
Individual work, demonstrations on the board without debate or discussion |
Cooperative |
Small group, centers, and workstations |
|
Search for correct answers |
Answer > process (only one correct process) |
No right or wrong answers |
Process (many correct processes) > answer |
|
Memorization of facts |
Formulas and equations |
Conceptual change |
Process and celebration of unique problem-solving methods |
|
Reliance on textbooks |
Vocabulary lists and reading passages precede context-building activities (if any) |
Students construct meanings |
Context before content; students first experience new content and then add academic vocabulary to speak about it in a common frame of reference |
|
Paper-and-pencil tests |
Traditional multiple choice tests |
Alternative assessment |
Decide-and-defend, discourse, games, and rubric-based evaluations |
Source: https://canvas.vt.edu/courses/62492/pages/traditional-vs-constructivist-classrooms
Teachers who take actions into consideration not only engage students with the content but tend to achieve higher academic results as well. This process takes time, though. “For significant learning, we need to revisit ideas, ponder them, try them out, play with them and use them” (Hein, 1991). It also takes motivation. Teachers who create interpersonal connections with students, elicit their background knowledge, and tailor lessons to their interests are more successful constructivist teachers.
In K-5 math teaching, we often use the analogy of a lifeguard to understand the role of a constructivist teacher. Imagine students at the pool learning new content: in this case, learning how to swim. The lifeguard provides students differentiated instruction and supports based on where they are in their learning process—some get a flotation aid, some stay at the shallow end, and others are ready to do flips off the diving board. Through modeling, discussion, partner and team sharing, and hands-on examples, the lifeguard facilitates the learning of the various students, providing parameters to maintain safety and order, but still allowing independent exploration and mastery. What the lifeguard does not do for the students is swim for them in order to teach them. Productive struggle is an integral part of context building and understanding of this new content.
This parallel can be drawn in our classrooms. Teachers provide learning experiences for students through differentiated activities, including 1:1 work with the teacher, group projects, and games. A teacher may also include a short mini-lesson to demonstrate a new technique or method of problem-solving, much like the lifeguard may include a mini-lesson on the breaststroke to model proper form. The teacher allows students to investigate, explore, and experience controlled failure in the classroom in order to learn, question, and embrace productive struggle. At no point should the teacher simply give students the answer and move on, assuming they understand the content. Instead, teachers celebrate the diversity of opinions, methods, and questions that arise from problem solving.
How does this actually play out in the classroom? What models for teaching through constructivism are there?
The CRA model
The CRA (concrete-representational-abstract) model is a powerful strategy for teaching new math concepts. It is a three-part constructivist process that transitions students from hands-on instruction to the symbolic math we use as adults. This brings both meaning and context for how and why we use math to solve problems. Since state assessments often require students to solve problems at all three levels, it has the additional benefit of helping them be successful in high-stakes testing. Specifically, research-based studies show that students who use concrete materials develop more precise and more comprehensive mental representations, often show more motivation and on-task behavior, understand mathematical ideas, and better apply these ideas to life situations.
How does each phase of the CRA work?
Concrete: In the first phase of the CRA, teachers select manipulatives (counting blocks, geometric shapes, unifix cubes, measurement tools, fraction bars, etc.) to demonstrate, model, and allow students to explore a new concept. This tactile approach helps ingrain the real-world meaning behind the math and provides kinesthetic learning for all students. A classic example is using baked goods such as a pizza or pie and cutting it into sections to understand fractions as part of a whole. In older grades, this may take the form of launching a rocket or shooting basketballs to see how parabolic arcs work and can be measured. Multiple different concrete models can be used to represent the same mathematical concept in order to encourage a variety of ways of thinking and spark classroom discourse.
Representational: Often called the semiconcrete or pictorial level, this phase transfers concrete models into visual representations using drawings and images. As adults, we often still rely on this phase while modeling complex problems (e.g., a floorplan for a house). To extend our previous examples, instead of a real pizza we would use a drawing of a pizza, substitute a fraction bar drawing for physical blocks, or draw a basketball’s trajectory rather than shooting hoops. During the representational phase, the teacher should encourage students to draw in a variety of different ways to promote the idea that there’s more than one right way to do math.
Abstract: The abstract phase is the symbolic level. Using operations and mathematical symbols, this phase would depict fractions numerically (e.g., 3/16) and parabolic arcs using an equation such as f(x) = a(x-b)^2 + c, where a is the slope, b is the distance from the basket, and c is the maximum height of the ball. Presenting the equation to students before they have encountered concrete and representational models would be confusing and carry little meaning, often inspiring the dreaded student question, “Why do I need to know this?” However, an equation provides a lot more granular information about the movement of the ball than a concrete or pictorial model can.
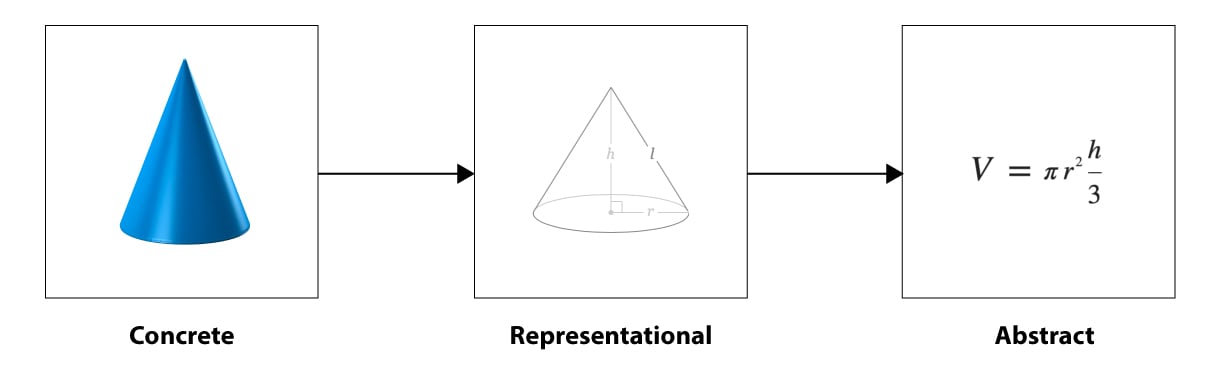
Taking the CRA one phase at a time helps bring context and real-world connection to the concepts students learn. CRA can also double as an intervention or acceleration strategy in that not all standards in a given grade level require students to be able to solve problems at the abstract (or representational) levels. Accordingly, struggling students can gain practice and understanding of new concepts by going back to a previous phase; advanced students can push ahead to a subsequent phase to extend their thinking. “When implementing this strategy, a teacher practices good instruction by referring to concepts or activities in the different states.” This cyclical approach reinforces learning. It also ensures that students don’t develop a conceptual misunderstanding before progressing to the next level. Still, CRA fits into a larger picture of instruction that we will explore next.
Mathematical modeling method
Mathematical modeling is a teaching technique that focuses on the investigation of real-world problems using mathematics as a tool to make sense of the situation and map out possible solutions. Throughout the process, students apply different strategies and evaluate their ability to solve the problem; students also make assumptions about the problem to help them decide which methods are best to use. We can think of mathematical modeling as being under the umbrella of problem-based learning, but with a math-specific focus. Students can model problems using all three CRA phases to integrate modeling with the instructional approach discussed above.
Teachers often specify limitations such as time, money, energy, distance, health, or safety to make the problem more realistic. Finding the “right” answer is not the mission—instead, students attempt to find the best solution within the confines of the scenario. “[R]ather than finding a perfect answer, the solutions are ‘good enough’ for the real-life requirements. These problems can be motivating for mathematics students, who can relate to mathematics that solves problems that are important to them.”
What other benefits are there?
For the fun of it: Learning mathematics as a procedure or rote memorization is boring and disconnected from reality. We know that when students are engaged in content, they learn more deeply, retain knowledge longer, and perform better on high-stakes tests. Although there is a time for learning equations and formulas and practicing using them to develop fluency, it should not be the only way to learn math.
Celebrating different approaches: We often think of math as having “just one right answer”; however, in the real world, complex mathematical models compete to provide optimal solutions (e.g., how to handle healthcare funding). Mathematical modeling engenders discourse, debate, and articulation of viewpoints. These are critical 21st-century skills that not only make your students better mathematicians as they learn from one another but also make them better stewards of our planet and better global citizens.
Improve understanding: It’s hard to understand why you should apply the quadratic formula, much less a cosine or tangent in the real world. Word problems often compound this issue, making it even harder to see the real-world connection. Mathematical modeling gives us a real-life situation and applies math to a problem from daily life, engineering, business, science, healthcare, or policy. These are the real unanswered questions in our lives. By using them, we can bring meaning to the equations, processes, and tools students have to learn to master the standards.
Productive struggle: Seldom do professionals in any math-related field “get it on the first try.” Solving problems is iterative, cooperative, and frustrating. Helping students understand that this is a natural and essential part of problem-solving helps them develop grit and perseverance. In education we think of this as productive struggle. The teacher facilitates the learning, but does not intervene. Rather, he or she questions, probes, and motivates students to try new approaches, look at what they’ve done in a new light, and understand that they are not failing but rather growing through the challenge.
Cooperative learning: We’ve already alluded to this, but it’s important to clearly state: complex problem solving requires a team. Students need to understand that in both their professional and personal lives, the help of others will be invaluable to producing better work and continuing to learn. Mathematical modeling requires that students discuss, share, and debate ideas in the process of problem solving and afterward, when comparing and contrasting models. There’s always something to learn from another.
How might a mathematical modeling lesson work in elementary grades? Snack time affords the perfect opportunity. Picture a snack break where your entire class gets goldfish crackers; they can be the rainbow variety to add interest or just plain ones to keep things simpler. A natural series of questions that may arise from students. How many total crackers are there? How do they get distributed evenly if they’re out of the package? Are they distributed to be precisely even or roughly even? Should they be distributed evenly or is there another method of sharing that may be better?
Depending on the grade level of the elementary student, there’s a wide range of mathematical models they can construct to begin answering these questions, from simple grouping and counting with visual models, to algebraic equations using multiplication and division, to hands-on models that weigh goldfish and use estimation. Each is a valid method; other methods exist and should be encouraged.
What’s important is that students set up assumptions and develop a means to address the problem(s) using concrete, representational, and/or abstract models. Along the way, students should refine their models with added information, facilitation support from the teacher, and group discussion. How students present to other students is just as important—graphics, data tables, and explanations are vital to a compelling model in the real world, so there’s every reason to use them here, too.
Nevertheless, mathematical modeling is not used in a vacuum. Prior to a problem-based activity like this one, students would have learned the mechanics of addition, subtraction, multiplication, division, estimation, weight, mass, etc. to aid them in constructing their models. Without this prior understanding, they would have no compass to guide their initial assumptions and plan. WIth that being said, the best way to use mathematical modeling is within a more holistic lesson model: the 5E. Where does it fit in? In the Explore and Elaborate sections.
The 5E lesson model
Developed in 1987 by BSCS, the 5E model has long been a cornerstone of constructivist learning. While it was originally used for science instruction, it can be seamlessly applied to math. The 5E model is often associated with inquiry-based learning, active learning, experiential learning, discovery learning, and knowledge building—all variations and parallels of constructivism. Split into five phases—Engage, Explore, Explain, Elaborate, and Evaluate—the 5E approach helps students build knowledge from prior understandings via context-building activities and differentiated learning.
It can be easy to assume that the 5E is a weekly lesson plan structure: Engage on Monday, Explore on Tuesday, and so forth. The reality is that the 5E is not a one-module-per-day teaching method; it is also not necessarily linear. In fact, proficient users of the 5E lesson model understand that the lesson may often take more than one week with Explore, Explain, and Elaborate occuring cyclically with chunked, or scaffolded, bites of content. For example, if we were to consider a standard such as the addition and subtraction of fractions, we may have an Explore hands-on lesson with manipulatives that first allows students to model this concretely. In turn, we would have an Explain that establishes the common ground vocabulary and discusses how students felt and thought about the exercises in the Explore. Afterwards, differentiation opportunities using a variety of modalities can be used so that each student can practice with the new learning before moving on to a new Explore that models the entire process through pictorial representations—and so the process begins anew. Below we examine each of the parts of the 5E and how they interconnect.
Engage
The Engage section is all about laying the foundation for learning. Teachers begin this section by pre-assessing students to determine their current understanding and how best to design the lesson to meet them there. A central activity—the Hook—then lays out a storyline narrative to establish a purpose for learning and to be used as a reference to return to throughout the entire lesson cycle. The Hook provides guidance and purpose for the rest of the lesson’s activities.
Explore
This is where students dig into the meat of the content. The Explore section provides scaffolded hands-on activities that build toward mastery of the standards. “Students are encouraged to apply process skills, such as observing, questioning, investigating, testing predictions, hypothesizing, and communicating, with other peers. This phase of the learning cycle tends to incorporate the main inquiry-based activity or experience, which encourages students to develop skills and concepts. The teacher’s role is one of facilitator or consultant. In addition, students are encouraged to work in a cooperative learning environment without direct instruction from the teacher.”
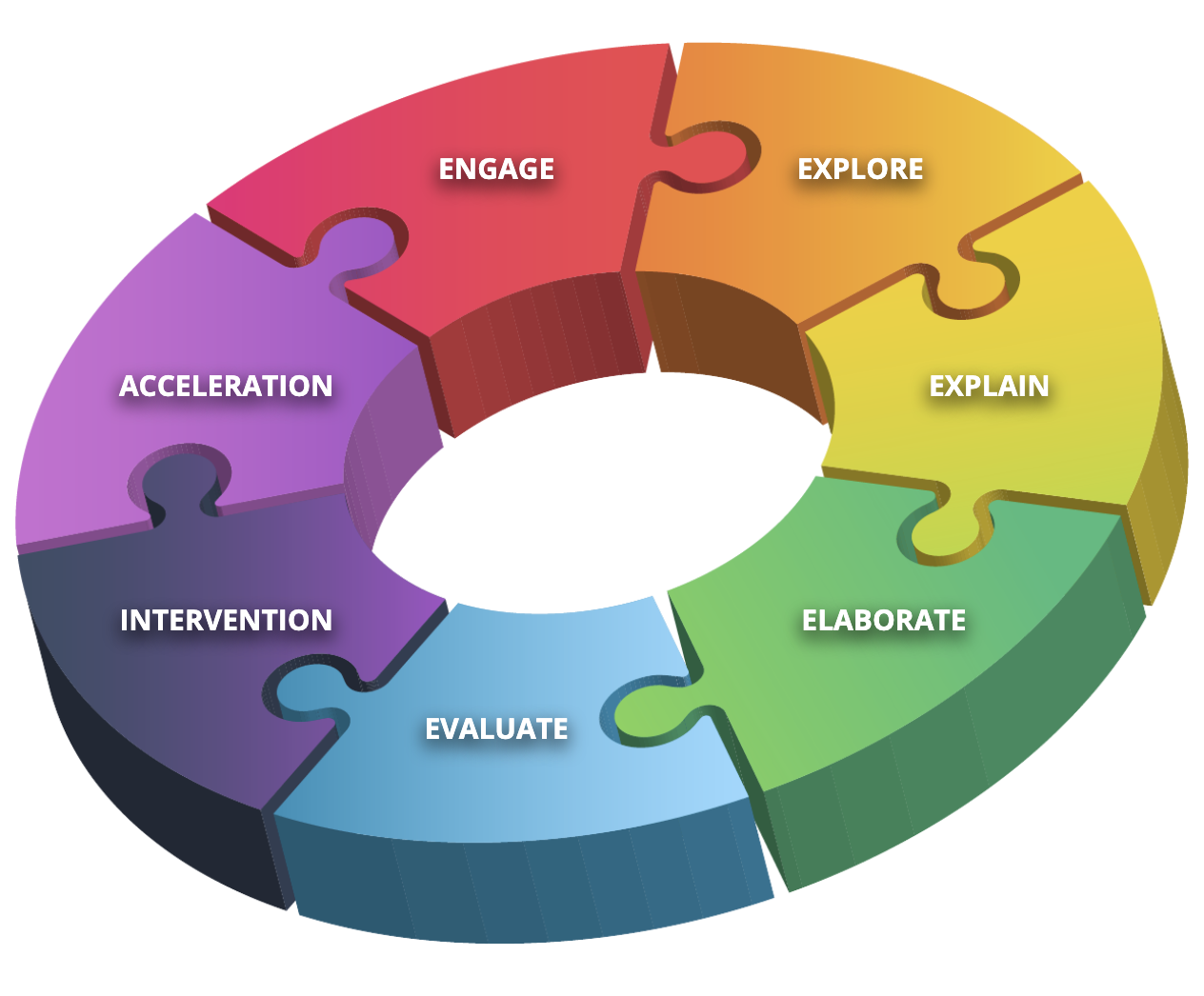
Explain
Paired with Explore, the Explain section offers a variety of resources that help connect the experiences of the Explore activities to the academic content students need to know. Resources to accomplish this may include illustrated vocabulary cards, independent practice, and journal prompts. These and other resources can be used to support the Explore activities and solidify student learning, prompt new questions, and develop a common academic language they can use to further apply the content to real-world problems.
Elaborate
Workstations are a go! The Elaborate section makes differentiation possible by leveraging a wide range of activities—digital and paper-based games, spiraled review, career connections, literacy connections, and research—that are perfect for rotations. These activities allow students to continue learning while you make time for small group interventions, reteaching, and independent acceleration projects to help both your struggling and advanced learners.
Evaluate
Get the data you need from the assessment tools provided in the Evaluate section. Nontraditional assessments such as portfolios, performance-based tasks, rubric-based activities, debates, journal logs, and portfolios are just as important as traditional fill-in-the-blank, multiple choice, and essay-driven assessments.
Many teachers elect to expand the use of the 5E model with Intervention and Acceleration to create the 5E+IA; however, it can be a little confusing to know when to use Intervention and Acceleration without training. Both of these modules should be infused throughout the 5E cycle—if a student is struggling or advanced, they should have the opportunity to receive direct support via Intervention resources or expand their thinking beyond the limitations of a standard with Acceleration activities.
Intervention
Useful during Elaborate or as an after-school support, Intervention often contains a small hands-on activity designed to target students’ conceptual misunderstanding while building their math skills. During Intervention, teachers should work with students 1:1 or with small groups in Tier 3 instructional support.
Acceleration
In the Acceleration section, students can engage in a design challenge or relate what they’re learning to current events around the world—activities that prompt them to think more deeply about the content and its applications and grow beyond the letter of the standard. This can also be a time when students teach other students in peer-to-peer instruction.
Implications for student learning
Research into constructivist learning has revealed two overarching benefits: increased problem-solving capacity and ownership over learning. Constructivist teachers find that their students develop increasingly complex mathematical structures, move further into the abstract, and become more capable of solving a wider array of math problems through a wider range of methods. Meanwhile students become more autonomous, more self-directed, and more engaged with mathematical learning. Students often realize that they discover math through doing and their own productive struggle than direct transmission from the teacher. This shift in perspective spurs students to take more and more ownership over their own learning.
Still, constructivism is not without its challenges. Classroom management, time, and equity are all issues. Many schools lack the materials to properly allow students to learn through hands-on instruction or may lack the time to conduct small group rotations and interventions in a standard teaching block. Teachers are thus forced to juggle a lot of variables to be exemplary constructivist teachers. On top of this, the pressure of high-stakes testing may compel teachers to focus more on test prep than quality instruction, thereby derailing constructivist learning.
Trust the data. Constructivist learning works and pays dividends on students' ability for their entire life. Students who learn through constructivist means perform well on high-stakes testing. Additionally, there are less obvious benefits to constructivist teaching and learning. Because self-discovery, sharing, communication, and context-building through background knowledge and real-world experience are cornerstones of the pedagogical system, students develop a wide variety of 21st-century skills as a result. Perhaps the most important of all is building resilience and grit in students. This self-confidence will permeate all facets of their lives, empowering students to take on challenges throughout their K-12 and professional careers.
References
Elliott, S.N., Kratochwill, T.R., Littlefield Cook, J. & Travers, J. (2000). Educational psychology: Effective teaching, effective learning (3rd ed.). Boston, MA: McGraw-Hill College.
Fox, R. (2001). Constructivism examined. Oxford review of education, 27(1), 23-35.
Hein, George E. (1991). Constructivist Learning Theory. Retrieved from
https://www.exploratorium.edu/education/ifi/constructivist-learning
Levy, Rachel. (2015). 5 Reasons to Teach Mathematical Modeling. Retrieved from
https://www.americanscientist.org/blog/macroscope/5-reasons-to-teach-mathematical-modeling
Wickstrom, Megan H. and Aytest, Tracy. (2018). Elementary Modeling: Connecting Counting With. Retrieved from
Clements, Douglas H. and Battista, Michael, T. (1990). Constructivist Learning and Teaching. Retrieved from

