Introduction
Most students love talking to each other during class, and most teachers find their chattiness to be exceedingly annoying and disruptive. However, it can also be a valuable teaching tool. With some patience and persistence, teachers can channel students’ chattiness into constructive conversations about math—a technique known as intentional discourse.
Intentional discourse is an exploratory approach to learning. Let’s imagine a grassy school playground, a place where students can interact with peers, express themselves, scrape their knees, and pick themselves back up. Now, picture a recess in which students can only march around a blacktop. The playground has rules, but affords great freedom, whereas the blacktop constricts students with rules. Intentional discourse parallels the structured freedom of the playground. Lecture-based instruction, on the other hand, accommodates only one kind of learning style, just as the blacktop allows for only one kind of exercise. By implementing intentional discourse in their classrooms, teachers can open a door to learning for all kinds of students. By implementing intentional discourse in their classrooms, teachers can open a door to learning for all kinds of students.
By implementing intentional discourse in their classrooms, teachers can open a door to learning for all kinds of students.
Interactive Learning and the Lecture-Based Classroom
In lecture-based classrooms, the teacher is the “sage on the stage” who transfers knowledge from herself to the students. In this construct, learning is passive. Students sit, listen, and absorb information, and successful students can demonstrate on a test that they received and stored the information. This mode of teaching and learning has dominated classrooms since its advent in early medieval European universities. In recent decades, however, it has come under scrutiny by education professionals. In one well-known article, a biology professor analyzed 225 studies focusing on methods for teaching STEM to undergraduates. “[He] concluded that teaching approaches that turned students into active participants rather than passive listeners reduced failure rates and boosted scores on exams by almost one-half a standard deviation.” That means there was a six percent difference between the grades of students who learned in lecture-based classrooms and those who learned in interactive ones.
Anyone who has sat through a lecture understands why lectures don’t work for many students. They are often boring, even for students interested in the subject matter, and so much depends on the charisma of the individual lecturer. Some teachers are clear communicators whose passion captivates and inspires. Yet many are dry, disorganized, or unenthusiastic. Moreover, the dazzling lectures of a bright and gifted speaker may discourage students with confidence issues. They may convince themselves that they simply “don’t have what takes” to learn material that the teacher has spent years mastering. Most teachers have heard some variation of “I’m just not smart enough” from a struggling student. A teacher who makes math look easy and natural may only reinforce the insecurities of a student who finds it to be complicated and foreign.
Intentional Discourse Methodology and Examples
Of course, pivoting away from lecture-based instruction is anything but easy. Moreover, some educators and scholars argue that “active learning” is a nebulous term that fails to prescribe any kind of practical methodology. Intentional discourse is a concrete step toward implementing active learning in the classroom.
Practicing intentional discourse, however, does not mean that we need to jettison the lecture entirely. On the contrary, intentional discourse complements the lecture by allowing students to process new content aloud.
But how do teachers facilitate intentional discourse? It’s always good for teachers to begin by asking themselves what classroom activities prompt discussion, how to organize those activities in a way that keeps the conversation focused on math, and who will do the talking. This three-pronged approach is known as “what-how-who.”
Consider, for example, a class that’s learning squared numbers. The teacher has spent the past few days explaining what squared numbers are and how to make them. Now, she wants her students to practice identifying them. She writes four numbers on the board: 9, 16, 43, and 25. She instructs the class to identify the number that does not belong and explain why it doesn’t. Clarice eagerly raises her hand and suggests that 16 doesn’t belong because it’s even. The teacher, in turn, asks the class what they think about Clarice’s answer. Tommy agrees that 16 is in fact the only even number but suggests that 43 doesn’t belong. “The numbers that aren’t 43 are the kind of numbers that you get when you multiply two of the same numbers,” he says. Seeing Tommy struggle with the terminology, Nancy blurts out, “43 is the only number that isn’t a squared number.” Now that the class has arrived at the correct answer together, the teacher divides the students into groups of four, instructing them to determine the square root of each number. In this example, the teacher answers each question in the who-how-what approach. She answers the “what” question by writing the numbers on the board, the “how” question with the prompt “What do you notice about the numbers?” and the “who” question by asking her students to raise their hands.
To facilitate intentional discourse, you can also follow teacher discourse moves (TDM). There are six TDMs:
- Waiting for students to think
- Inviting student participation
- Revoicing students’ responses
- Asking students to revoice their peers’ responses
- Probing students’ thinking
- Creating opportunities for students to engage each others’ reasoning
To see the TDMs in action, let’s imagine a teacher who’s acclimating her students to using letters as mathematical symbols. She draws the following image on the board:
A few eager students already have their hands raised as soon as she finishes her drawing. She tells them to wait for everyone to observe the square and write down a few sentences about what they think the letters mean and how they relate to the numbers. After a few minutes, she invites students to share their observations.
Despite varying personalities and abilities, most of the students participate. Santiago, who’s reserved but inquisitive, reads directly from the page: “I think the letters are like money, and the numbers mean how many kinds of money you have.” Seeing that Santiago is on the right course, the teacher revoices his answer: “So, class, what I’m hearing from Santiago is that the letters represent different kinds of money, like dollars and coins. And the numbers tell us how many of each kind of dollar or coin we have. Anything else you notice?” Angela, who sits a few desks behind Santiago, says, “Maybe the letters mean different kinds of cents, but not like dollar bills.” At these words, Tim raises his hand, but before the teacher calls on him, he begins revoicing Angela’s answer, “I think some of the letters represent specific coins. Like the “Q” means quarters, the “N” means nickels, but the “D” means dollars.” The teacher probes his thinking by asking him to explain his reasoning. “Well, you said the letters mean money,” he begins. “‘Quarter’ and ‘nickel’ are the only kind of money that begin with ‘Q’ and ‘N,’ and ‘dollars begins with ‘D.’” To give the class an opportunity to engage with Tim’s reasoning, the teacher asks, “Class, what do you think of Tim’s answer?” When the teacher calls on Samatha, she says, “I think Tim is right about the ‘N’ and the ‘Q,’ but I think that the ‘D’ means dimes because the ‘N’ and the ‘Q’ are both coins and so the ‘D’ should also be a coin.” Aided by their teacher, the class arrives at the right answer through a collective effort. Although it may seem that intentional discourse relies on verbal communication, it can also incorporate elaborate visual demonstrations. For example, “bansho,” which means blackboard writing in Japanese, is one visual technique that can spark mathematical dialogue. In bansho exercises, students solve problems individually, and the teacher chooses two to four solutions to tape on the board. Here’s what the final product looks like:
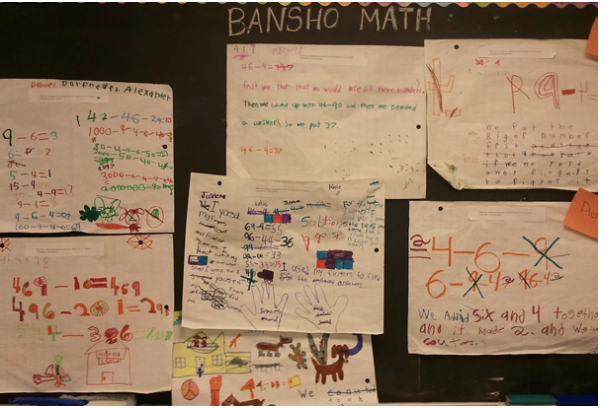
The chosen solutions should be correct but should also vary in approach, and some solutions will be cleaner and more efficient than others. Indeed, one goal of bansho is to introduce different kinds of mathematical thinking. After taping their solutions on the board, the students whose solutions were selected discuss their mathematical thinking in front of their peers, who in turn make comments and ask questions. As the conversation unfolds, the teacher makes notes about misunderstandings, opportunities to elaborate, and overlaps between students’ mathematical thinking. Bansho gives students a bird’s-eye view of mathematical methodology. As they discuss the solutions, they can contrast the different approaches displayed next to each other on the board.
A gallery walk is another excellent way to facilitate intentional discourse. A gallery walk does not actually require any walking (although it can if you want). The point of a gallery is for students to view each other’s work. Students solve problems individually and comment on each other’s solutions with sticky notes. Alternatively, students can solve a problem together in small groups. In both cases, they interact with each other’s work by writing or talking. Teachers can take the gallery walk a step further by having the students condense the comments into a succinct presentation. Students practice sifting through information, sorting what is useful from what is unhelpful. As students identify comments that help them improve their mathematical thinking, they develop an eye for constructive feedback.
Students will usually feel more comfortable talking about math in the context of familiar subjects, such as sports, popular culture, and everyday experiences. This approach is known as real-world connection. Consider, for example, a middle school math teacher who’s trying to motivate an underperforming student. He’s a star athlete who loves being part of the football team and adores the Houston Texans. His below-average math grades threaten his eligibility, forcing him to attend tutoring. The teacher uses these tutoring sessions to tailor the math content to his interests. She decides to print out the Texans’ win/loss record from 2017, 2018, and 2019. She starts by asking him what he notices: “The Texans won a lot more games in 2018 and 2019 than in 2017.” Without the teacher prompting him, he continues: “It’s because Deshaun Watson got hurt in 2017 and was healthy for all of 2018 and 2019.” “Good observation,” the teacher says. “Now, based on these two seasons, let’s use math to figure out the likelihood of the Texans winning the Super Bowl with and without Deshaun Watson in 2020.” This student already spends much of his time talking about the upcoming season and making predictions. It’s something he cares about, so naturally he will put forth the effort to learn the math that will make his predictions more accurate.
Benefits of Intentional Discourse
In personal and professional life, adults must solve problems together. Successful problem-solving is, in part, accomplished through effective communication, and intentional discourse lets students practice problem-solving through communication in a safe place, where they can learn from their mistakes.
Imagine, for example, an elementary class that’s learning multiplication and division. Every day the cafeteria staff delivers goldfish to the class for snack time. One day during snack time, the teacher divides the students into small groups and asks them to count out 28 goldfish on a plate. As part of a CRA lesson plan, she instructs them to work together to figure out how many ways you can divide 28, using the goldfish. In Group A, Joana, who’s memorized the times table, recites the numbers by which 28 can be divided. Rashard reminds her that the teacher told them to use the goldfish. After some discussion, they agree that they should start by splitting the goldfish in half, which gives them two groups of 14. Samara suggests that they halve the two groups since 14 is an even number and can, therefore, be divided in half evenly.
Joanna then attempts to half the four groups of seven, but realizes that she can’t do so without breaking a goldfish in each group. Rashard, who has been recording the number of goldfish in each group, reads his numbers to the group: “28 goldfish are divisible by fourteen, two, seven, and four.” The group has worked together to accomplish the task, which offered Joanna a valuable lesson. Even though she can recite the times tables, that doesn’t mean she can apply her knowledge to solve a problem in an unfamiliar context.
Intentional discourse lends itself to constructivism, a theory suggesting that people learn best through experience and by reflecting on their experiences. The abstract quality of math makes the subject particularly difficult to teach. It’s the reason so many students ask, “When am I ever going to use this?” A constructivist approach shows students how math fits into their lives. The value of math is, therefore, less likely to be questioned.
Intentional discourse also assimilates mathematical concepts naturally and subtly into students’ experiences. Let’s say it’s October, and a teacher is introducing his students to variables. Students have been talking about horror movies and Halloween costumes, so he asks his students to pretend that they are trying to escape a castle full of vampires, and their only defense is a slingshot for launching garlic. They have three bulbs of garlic with 12 cloves each. It takes at least three cloves to repel a single vampire, but we don’t know how many vampires stalk the castle.
For now, the teacher wants his students to identify the unknown variable. “Class, remember yesterday when we talked about how letters can represent numbers that we are unsure of. In our vampire-castle scenario, what would “x” represent?” Intrigued by this spooky quandary, students eagerly offer answers. Rosemary suggests that “x” represents the number of hallways we have to walk through to escape. Her explanation is simple: “We don’t know how many hallways we have to walk through.” The teacher then asks the class, “Rosemary is right, but tell me, what do we know about the situation.” Ragan says that we only know how much garlic we have and how much it takes to ward off a single vampire. At this, Rosemary’s face lights up: “X’ represents the number of vampires because that’s what we don’t know about the situation,” she says. Ragan’s answer pointed Rosemary in the right direction. Rosemary not only learned from a classmate, she also kept trying even after she answered incorrectly. Intentional discourse should create an environment where students feel comfortable failing and learning from their mistakes.
Conclusion
Most educators don’t want students to recite what they’ve heard and read in class. They want them to engage with it and feel like they have something important to say. Intentional discourse gives students the freedom to articulate their thoughts as they solve problems. It not only promotes a culture of active learning, it helps produce a society of independent thinkers.